前端开发和网页设计/seo索引擎优化

内积与正交（Orthogonal Vectors） 

         已知两个向量x,y（如下图），怎么判断他们是否垂直呢？或者说，怎么知道他们的夹角是不是等于90°呢？

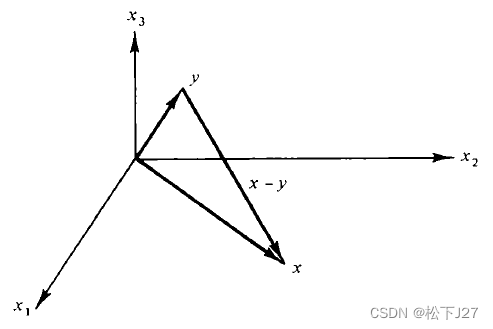
        在一个二维平面内，我们可以用上面的Pythagoras定理来描述。一般的，对中的两个向量，我们可以从他们共有的一个平面入手。在这个平面内，如果x垂直于y，x,y就构成了一个直角三角形，根据Pythagoras定理，则下面的公式一定成立：

 接下来，再根据向量的长度的计算公式，得到：

 进一步，我们得到等式的右边为：

  消去等式两端的共有项后，最终得到：

        上式我们可以写成一个1xn矩阵(列向量x的转置)和一个nx1矩阵(列向量y)的乘积, 即列向量x与列向量y的内积，也叫点积。

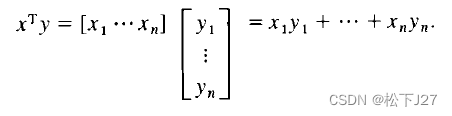
        因此，我们得出结论，在中的任意两个列向量x,y，如果正交（垂直），那么他们的内积为0。即：

=0 

 因此，我们说：

两个向量的内积为0是勾股定理在向量空间中的另一种表现形式。

同时，我们还得出，对于单个向量而言，向量的长度的平方等于他与自己的内积，即:

（全文完）

作者 --- 松下J27

格言摘抄：忠不忠，看行动！（无名氏）

参考文献（鸣谢）：

1，《Introduction to Linear Algebra》,5th Edition - Gilbert Strang

 2，线性代数及其应用，侯自新，南开大学出版社，1990.

文中截图均来自于上述文献。

 （配图与本文无关）

版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27​