您现在的位置是:主页 > news > 网站建设开源项目github/qq群引流推广平台免费
网站建设开源项目github/qq群引流推广平台免费
![]() admin2025/5/6 12:52:04【news】
admin2025/5/6 12:52:04【news】
简介网站建设开源项目github,qq群引流推广平台免费,网站已经克隆好了 怎么做仿站,资兴网站建设题目: 输入输出: 分析: 题目所要求的是小数第n位及其后面的两位,可以转化为求如下的结果: ansab∗10n2mod1000ans \dfrac{a}{b} * 10^{n2}\quad mod\quad1000ansba∗10n2mod1000 但是此时上述公式中存在 a/b&#…
题目:
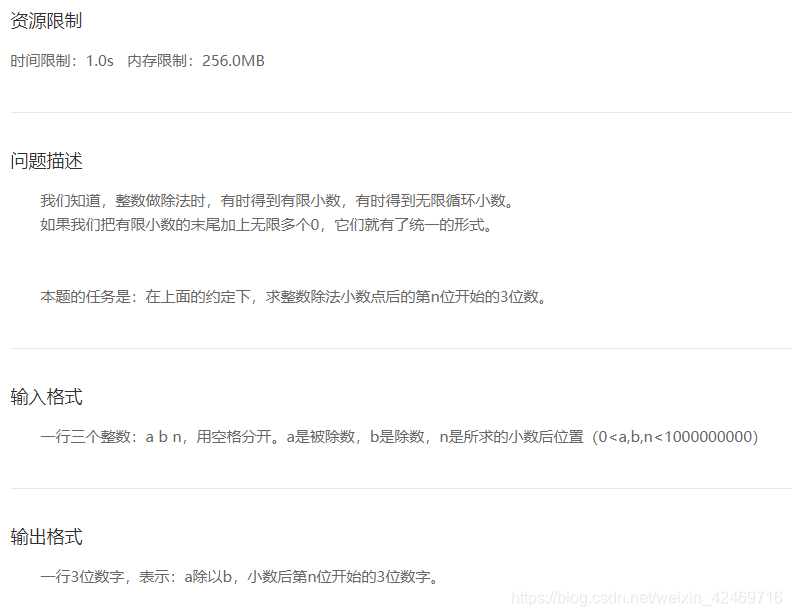
输入输出:
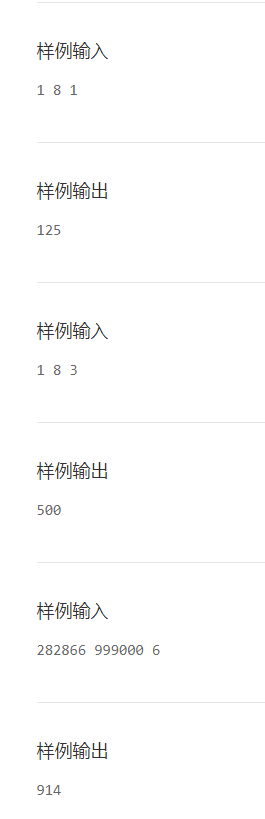
分析:
题目所要求的是小数第n位及其后面的两位,可以转化为求如下的结果:
ans=ab∗10n+2mod1000ans = \dfrac{a}{b} * 10^{n+2}\quad mod\quad1000ans=ba∗10n+2mod1000
但是此时上述公式中存在 a/b,此时精度肯定无法保证,因此要用到下述的替换公式:
abmodd=amodb∗db\dfrac{a}{b}\quad mod\quad d = \dfrac{a\quad mod\quad b*d}{b}bamodd=bamodb∗d
那么刚开始的等式就可以转换为下述公式:
ab∗10n+2mod1000=a∗10n+2modb∗1000b\dfrac{a}{b} * 10^{n+2}\quad mod\quad1000 = \dfrac{a*10^{n+2}\quad mod\quad b*1000}{b}ba∗10n+2mod1000=ba∗10n+2modb∗1000
此时应用上述问题就不会担心精度问题,但是此时直接计算 10n+210^{n+2}10n+2 还是会超时,所以此时我们要使用快速幂来进行解决
代码:
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;long long a,b,n,mod,ans;long long QuickMul(long long x,long long y,long long MOD)
{long long res = 1;while(y){if(y&1)res = res * x % MOD;x = x * x % MOD;y = (y>>1);}return res;
}int main()
{scanf("%lld%lld%lld",&a,&b,&n);mod = b*1000;ans = (a % mod) * QuickMul(10,n+2,mod) % mod / b;printf("%lld\n",ans);return 0;
}







