什么视频网站可以做链接地址/搜狗引擎搜索

摘录自：R语言实战 作者：王小宁、刘撷芯、黄俊文等译 仅用学习使用
该系列文章期待用一点一点和大家一起把R语言实战学习完~使自己的R语言和统计水平更上一层楼

接上一篇：R语言统计-回归篇：简单线性回归，上一篇主要讲了简单线性回归，这一篇咱们主要讲多项式回归和多元线性回归。

多项式回归

图8-1表明，你可以通过添加一个二次项（即

）来提高回归的预测精度。 如下代码可以拟合含二次项的等式：

fit2 <- lm(weight ~ height + I(height^2), data=women) 

I(height^2)表示向预测等式添加一个身高的平方项。I函数将括号的内容看作R的一个常规表 达式。因为^（参见表8-2）符号在表达式中有特殊的含义，会调用你并不需要的东西，所以此处必须要用这个函数。

> fit2 <- lm(weight ~ height + I(height^2), data=women)
> summary(fit2)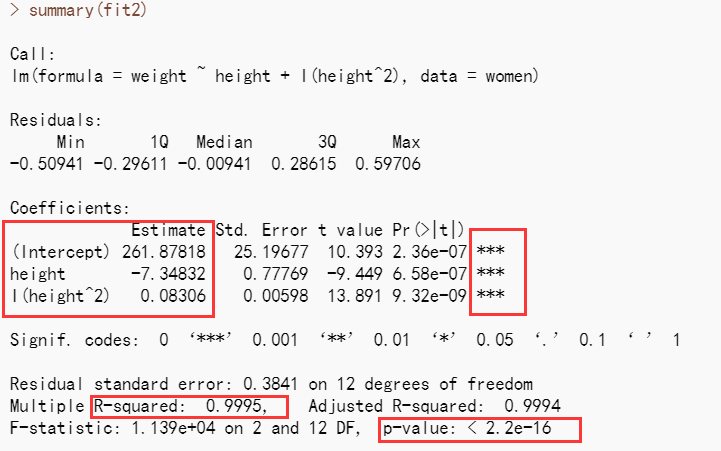 

plot(women$height,women$weight,xlab="Height (in inches)",ylab="Weight (in lbs)")
#添加拟合值对women$height的散点图并连线 fitted函数列出拟合模型的预测值
lines(women$height,fitted(fit2))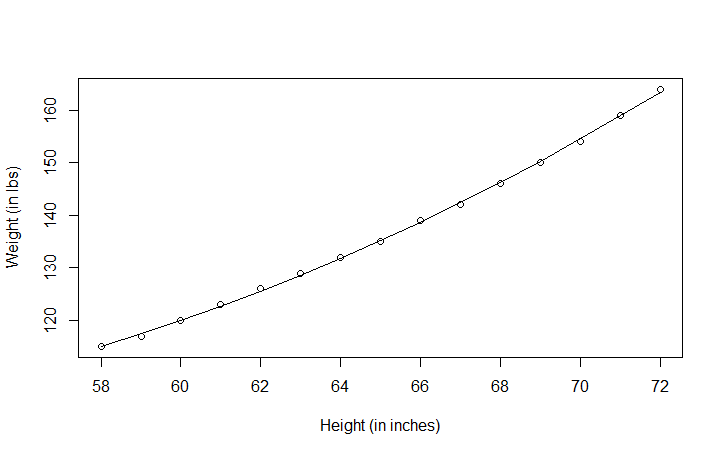 

新的预测等式为：

在p<0.001水平下，回归系数都非常显著。模型的方差解释率已经增加到了99.9%。二次项的 显著性（t=13.89，p<0.001）表明包含二次项提高了模型的拟合度。从图8-2也可以看出曲线确实拟合得较好。

一般来说，n次多项式生成一个n–1个弯曲的曲线。拟合三次多项式，可用：

#可以看到更加精细的刻画
fit3 <- lm(weight ~ height + I(height^2) +I(height^3), data=women)

虽然更高次的多项式也可用，但我发现使用比三次更高的项几乎没有必要。 在继续下文之前，我还要提及car包中的scatterplot()函数，它可以很容易、方便地绘制二元关系图。以下代码能生成图8-3所示的图形：

这个功能加强的图形，既提供了身高与体重的散点图、线性拟合曲线和平滑拟合（loess）曲 线，还在相应边界展示了每个变量的箱线图。spread=FALSE选项删除了残差正负均方根在平滑 曲线上的展开和非对称信息。smoother.args=list(lty=2)选项设置loess拟合曲线为虚线。 pch=19选项设置点为实心圆（默认为空心圆）。粗略地看一下图8-3可知，两个变量基本对称，曲线拟合得比直线更好。

多元线性回归

当预测变量不止一个时，简单线性回归就变成了多元线性回归，分析也稍微复杂些。从技术 上来说，多项式回归可以算是多元线性回归的特例：二次回归有两个预测变量（

和

），三次回归有三个预测变量（

，

和

）。现在让我们看一个更一般的例子。 以基础包中的state.x77数据集为例，我们想探究一个州的犯罪率和其他因素的关系，包括 人口、文盲率、平均收入和结霜天数（温度在冰点以下的平均天数）。 因为lm()函数需要一个数据框（state.x77数据集是矩阵），为了以后处理方便，你需要做如下转化：

states <- as.data.frame(state.x77[,c("Murder", "Population","Illiteracy", "Income", "Frost")])

这行代码创建了一个名为states的数据框，包含了我们感兴趣的变量。本章的余下部分，我们 都将使用这个新的数据框。

多元回归分析中，第一步最好检查一下变量间的相关性。cor()函数提供了二变量之间的相关系数，car包中scatterplotMatrix()函数则会生成散点图矩阵（参见代码清单8-3和图8-4）。

 #看相关性
cor(states)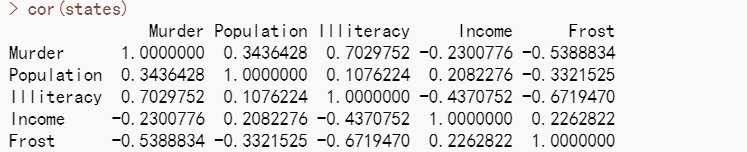

library(car)
scatterplotMatrix(states, spread=FALSE, smoother.args=list(lty=2),main="Scatter Plot Matrix")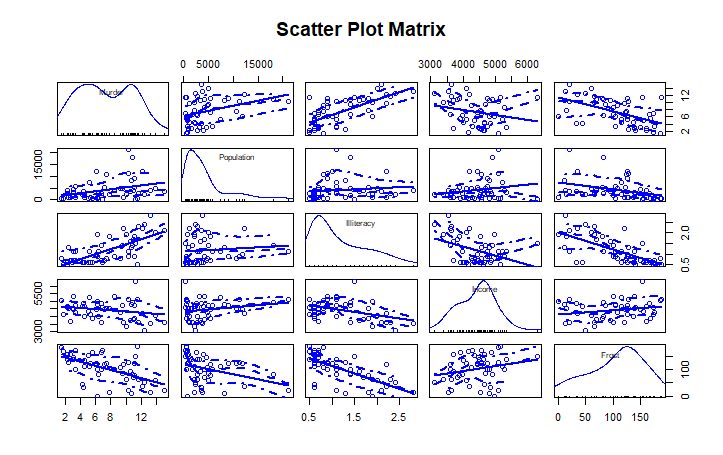 

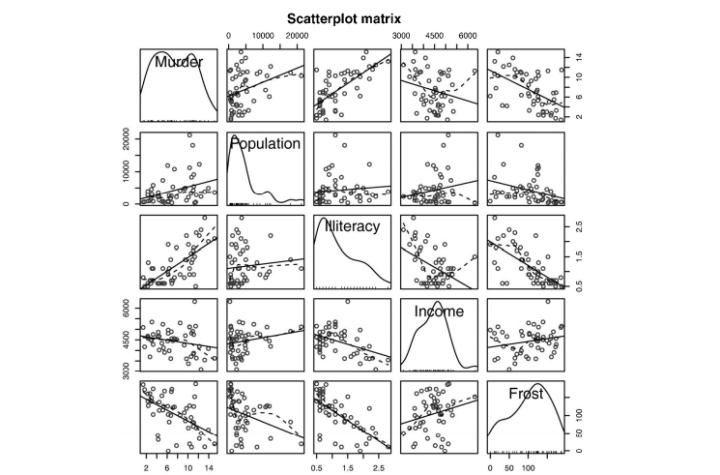
scatterplotMatrix()函数默认在非对角线区域绘制变量间的散点图，并添加平滑和线性 拟合曲线。对角线区域绘制每个变量的密度图和轴须图。

从图中可以看到，谋杀率是双峰的曲线，每个预测变量都一定程度上出现了偏斜。谋杀率随着人口和文盲率的增加而增加，随着收入水平和结霜天数增加而下降。同时，越冷的州府文盲率 越低，收入水平越高。

现在使用lm()函数拟合多元线性回归模型：

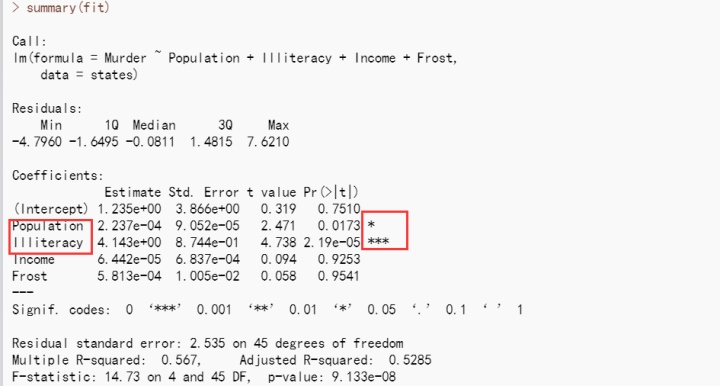
当预测变量不止一个时，回归系数的含义为：一个预测变量增加一个单位，其他预测变量保 持不变时，因变量将要增加的数量。例如本例中，文盲率的回归系数为4.14，表示控制人口、收 入和温度不变时，文盲率上升1%，谋杀率将会上升4.14%，它的系数在p<0.001的水平下显著不 为0。相反，Frost的系数没有显著不为0（p=0.954），表明当控制其他变量不变时，Frost与Murder 不呈线性相关。总体来看，所有的预测变量解释了各州谋杀率57%的方差。

以上分析中，我们没有考虑预测变量的交互项。在接下来的一节中，我们将考虑一个包含此 因素的例子。

有交互项的多元线性回归

许多很有趣的研究都会涉及交互项的预测变量。以mtcars数据框中的汽车数据为例，若你 对汽车重量和马力感兴趣，可以把它们作为预测变量，并包含交互项来拟合回归模型。

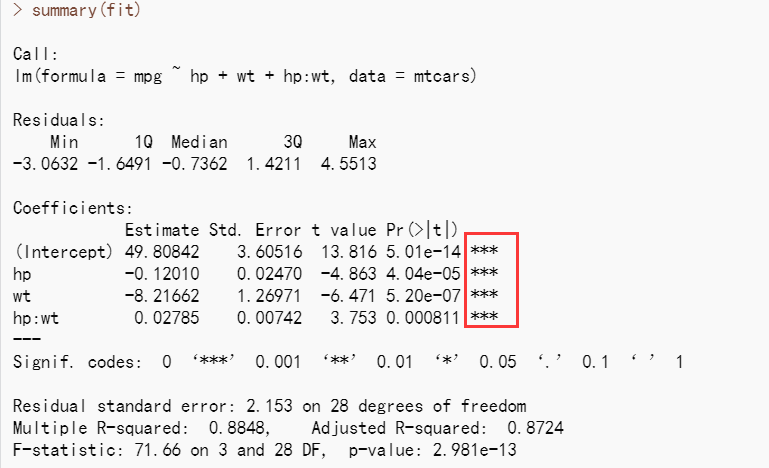
你可以看到Pr(>|t|)栏中，马力与车重的交互项是显著的，这意味着什么呢？若两个预测变量的交互项显著，说明响应变量与其中一个预测变量的关系依赖于另外一个预测变量的水平。 因此此例说明，每加仑汽油行驶英里数与汽车马力的关系依车重不同而不同。

预测mpg的模型为

。为更好地理解交互项，你可以赋给wt不同的值，并简化等式。例如，可以试试wt的均值（3.2），少于均值一个标准差和多于均值一个标准差的值（分别是 2.2 和 4.2 ）。 若

plot(effect(term, mod,, xlevels), multiline=TRUE)

term即模型要画的项，mod为通过lm()拟合的模型，xlevels是一个列表，指定变量要设定的常量值，multiline=TRUE选项表示添加相应直线。对于上例，即：

library(effects)
plot(effect("hp:wt", fit,, list(wt=c(2.2,3.2,4.2))), multiline=TRUE) 

结果展示在图8-5中。 从图中可以很清晰地看出，随着车重的增加，马力与每加仑汽油行驶英里数的关系减弱了。 当wt=4.2时，直线几乎是水平的，表明随着hp的增加，mpg不会发生改变。 然而，拟合模型只不过是分析的第一步，一旦拟合了回归模型，在信心十足地进行推断之前，必须对方法中暗含的统计假设进行检验。这正是下节的主题。