泰森多边形（Voronoi图）的matlab绘制

1.泰森多边形的介绍

泰森多边形是对空间平面的一种剖分，其特点是多边形内的任何位置离该多边形的样点（如居民点）的距离最近，离相邻多边形内样点的距离远，且每个多边形内含且仅包含一个样点。由于泰森多边形在空间剖分上的等分性特征，因此可用于解决最近点、最小封闭圆等问题，以及许多空间分析问题，如邻接、接近度和可达性分析等。

泰森多边形的构建可以分为2个步骤，1是Delaunay三角网的构建，2是三角网格外接圆心得连线。

在上一片文章中我已经介绍了Delaunay三角网实现的原理，所以这篇文章主要介绍一下如何利用已经构建的Delaunay三角网绘制Voronoi图。

二维Delaunay（德洛内）三角网的matlab实现 https://blog.csdn.net/weixin_42943114/article/details/82262122

彩色的Voronoi图算法参见：https://blog.csdn.net/weixin_42943114/article/details/82461228

2.算法实现

2.0 matlab自带函数算法

%采用matlab自带的函数进行绘制
clear
xdot=gallery('uniformdata',[200 2],5);
%delaunay三角形
figure(1)
DT=delaunayTriangulation(xdot);
triplot(DT,'color','k')
%voronoi三角形
figure(2)
voronoi(xdot(:,1),xdot(:,2));
xlim([0,1])
ylim([0,1])

2.1 Delaunay三角算法

首先是上一篇文章的Delaunay三角伪算法：

input: 顶点列表(vertices)　　　　　　　　　　　　　　　　　　　　  　//vertices为外部生成的随机或乱序顶点列表
output:已确定的三角形列表(triangles)初始化顶点列表创建索引列表(indices = new Array(vertices.length))　　　　//indices数组中的值为0,1,2,3,......,vertices.length-1基于vertices中的顶点x坐标对indices进行sort　　  　　　　　  //sort后的indices值顺序为顶点坐标x从小到大排序（也可对y坐标，本例中针对x坐标）确定超级三角形将超级三角形保存至未确定三角形列表（temp triangles）将超级三角形push到triangles列表遍历基于indices顺序的vertices中每一个点　　　　　　　　　  　//基于indices后，则顶点则是由x从小到大出现初始化边缓存数组（edge buffer）遍历temp triangles中的每一个三角形计算该三角形的圆心和半径如果该点在外接圆的右侧则该三角形为Delaunay三角形，保存到triangles并在temp里去除掉跳过如果该点在外接圆外（即也不是外接圆右侧）则该三角形为不确定        　　　　　　　　　     //后面会在问题中讨论跳过如果该点在外接圆内则该三角形不为Delaunay三角形将三边保存至edge buffer在temp中去除掉该三角形对edge buffer进行去重将edge buffer中的边与当前的点进行组合成若干三角形并保存至temp triangles中将triangles与temp triangles进行合并除去与超级三角形有关的三角形
end

算法最终输出的三角形列表trimat包含三个点的编号。
算法来源参见如下：
三角剖分算法(delaunay) http://www.cnblogs.com/zhiyishou/p/4430017.html
###2.2 Delaunay三角算法的凸边形检测
之后对上述算法得到的三角形网格的边缘进行进一步处理，使得图像变为凸型

输入上一算法中得到的trimat更新三角网格边缘三角形border_trimat更新三角网格边缘点border_point更新三角形网格之间的关系，即与每个三角形相邻的三角形trimat_con整理边缘点border_point顺序，使得顺时针（或逆时针）成为当前图像最外边缘依次循环边缘点的每一个点j按顺时针（或逆时针）做该点j与间隔点j+2的线段（border_point的顺序）求线段与点j+1相关的所有线段（或延长线）是否相交如果相交该点为图形边缘的突出点，忽略如果与所有点j+1相关的线段（或延长线）不相交该点为图形边缘凹陷点，连接返回最开始更新步骤输出trimat_con

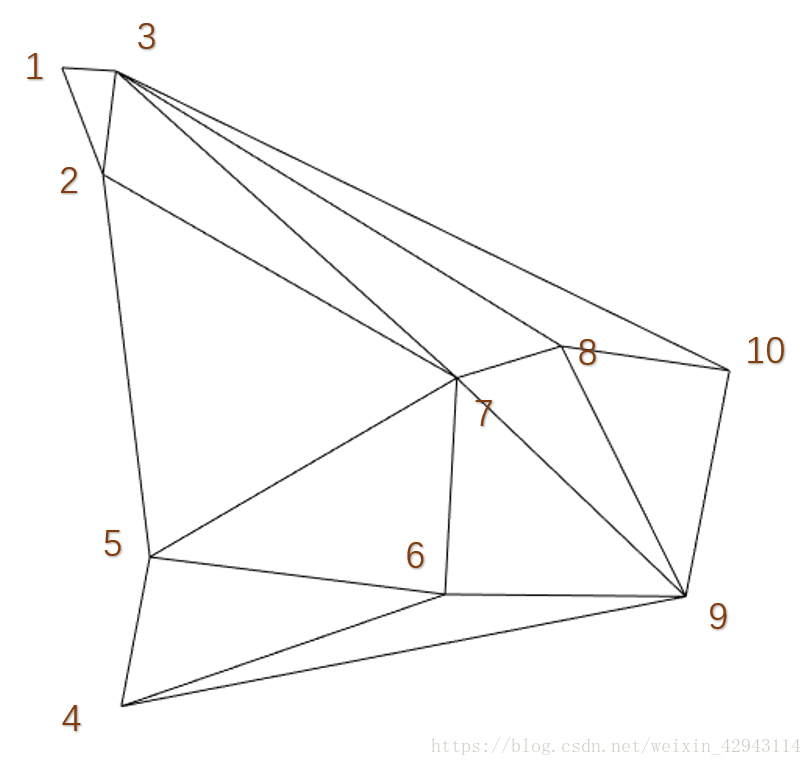
之后拿一个图形做例子，这是没有进行凸型检测之前的Delaunay三角网

三角网格的边缘点border_point为[3 1;1 2;2 5;5 4;4 9;9 10;10 3;3 1]，构成了首尾相连的一串边缘点。
检测线段32，中间点为1，1相关的线段只有12和13，与线段32重复，是突出点
检测线段15，中间点为2，2相关的线段有21、23、27、25，跑去15重复剩下23和27，线段15与23和27的射线都不相交，所以线段15是一个有效线段，2是凹点。连接线段15，更新border_point。

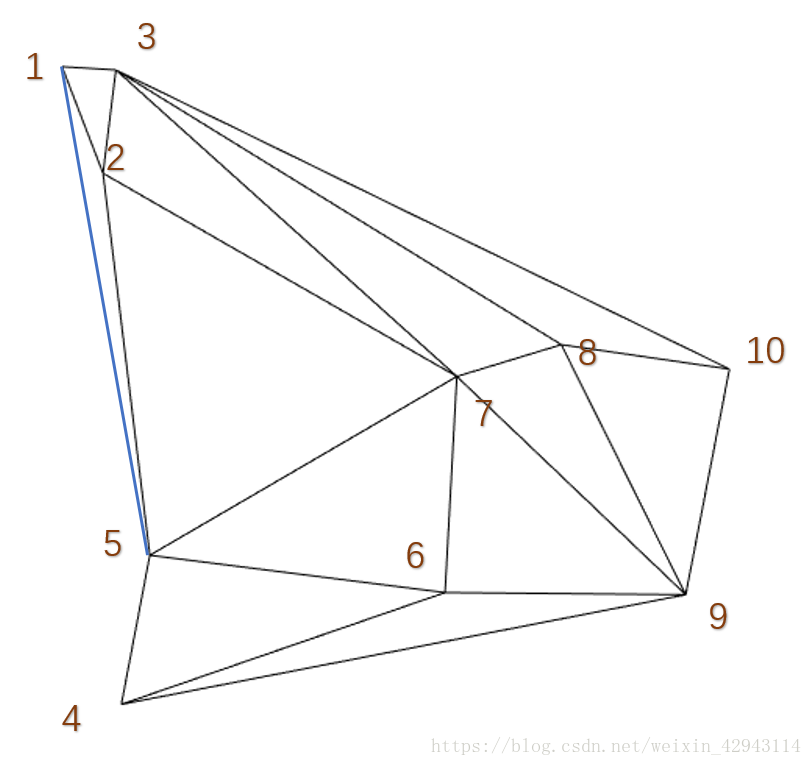
更新一次的三角网格如下

三角网格的边缘点border_point为[3 1;1 5;5 4;4 9;9 10;10 3;3 1]
检测线段35，中间点是1，1相关线段有13、12、15，删掉35重复的，剩下12。线段35和射线12相交（注：和线段12不相交但和射线12相交），所以35不是有效线段，1是凸点，忽略。
检测线段14，中间点是5，5相关线段有51、52、57、56、54，抛去14重复的，都不相交，说明14是有效线段。连接线段14，更新border_point。

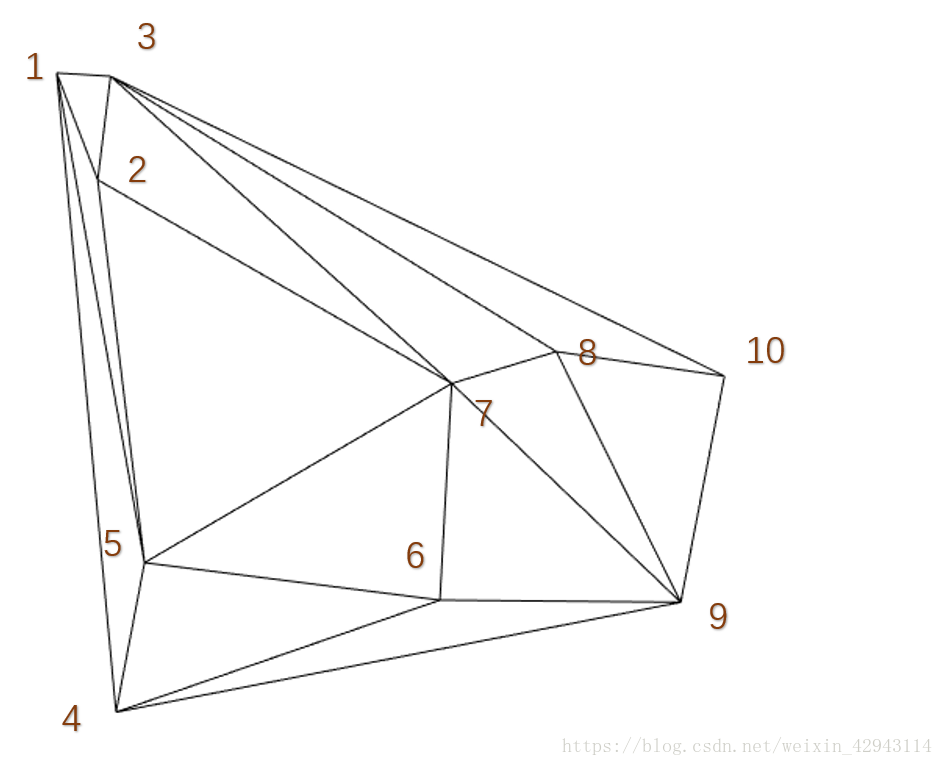
更新后的图像如下：

三角网格的边缘点border_point为[3 1;1 4;4 9;9 10;10 3;3 1]
然后依次循环3-4、1-9、4-10、9-3、10-1，发现都相交
所以这个图形是凸边形，结束循环。

这部分的代码如下：

%凸包监测
%思路是先找出边缘点（三角形只有1个或2个的），顺便整出一个三角形相互关系图，以后用。
%然后顺时针，依次隔一个点连接出一条线段，如果这个和之前的线段相交，则不算；如果不交，则记录出三角形
%更新完了以后，再监测一遍，直到没有新的为止。t_w=0;
while t_w==0[~,border_point,~]=makebordertri(trimat);border_point=[border_point;border_point(1,:)];temp_edgemat=[];temp_trimat=[];for j=1:size(border_point,1)-1tempboderedge=[border_point(j,1),border_point(j+1,2)];tempboderdot=border_point(j,2);%寻找带tempboderdot的所有边tempdotex=edgemat(logical(sum(edgemat==tempboderdot,2)),:);%删除相邻边tempdotex(ismember(tempdotex,[tempboderdot,tempboderedge(1)],'rows'),:)=[];tempdotex(ismember(tempdotex,[tempboderedge(1),tempboderdot],'rows'),:)=[];tempdotex(ismember(tempdotex,[tempboderdot,tempboderedge(2)],'rows'),:)=[];tempdotex(ismember(tempdotex,[tempboderedge(2),tempboderdot],'rows'),:)=[];%检测tempdotex是否为空，如果是证明不用相连t_N=size(tempdotex,1);t_t=0;if t_N>0%依次检测是否相交，只要有一个相交就不算；如果都不想交，则相连for k=1:t_Nif tempdotex(k,1)==tempboderdott_xdotno4=tempdotex(k,2);elset_xdotno4=tempdotex(k,1);endtt_xdotno4=xdot(t_xdotno4,:)-xdot(tempboderdot,:);xdotno4=xdot(tempboderdot,:)+tt_xdotno4/sqrt(sum(tt_xdotno4.^2))*(sqrt((xmax-xmin)^2+(ymax-ymin)^2));panduan=crossornot(xdot(tempboderedge(1),:),xdot(tempboderedge(2),:),xdot(tempboderdot,:),xdotno4);if panduan==1t_t=t_t+1;breakendend%t_t大于0说明有相交的线,略过if t_t==0temp_edgemat=[temp_edgemat;tempboderedge];temp_trimat=[temp_trimat;[tempboderedge,tempboderdot]];breakendendendtrimat=[trimat;temp_trimat];edgemat=[edgemat;temp_edgemat];%删除重复的三角形trimat=sort(trimat,2);trimat=unique(trimat,'stable','rows');if j==size(border_point,1)-1t_w=1;end
end

2.3 泰森多边形算法

这里泰森多边形的每一个顶点都是Delaunay三角网格的外接圆圆心，所以这一步的算法就简单很多:
1.求出所有三角形的外接圆圆心
2:按照三角形之间的关系依次连接各个圆心

如果遇到边缘点，只需要过圆心做三角形边缘线段中垂线即可，最终到图形边界为止。当然也可以做足够大的三角网格，做泰森多边形之后取一部分即可。

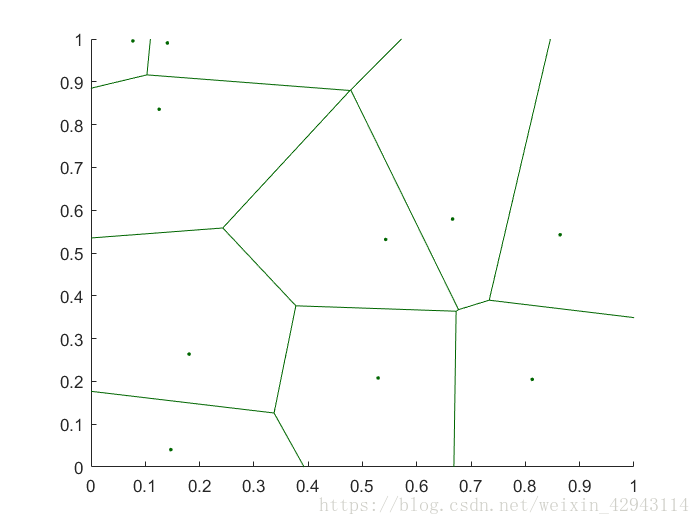
上一步中得到的图形做泰森多边形得到图形如下：

3泰森多边形的最终程序

最终matlab实现程序如下图所示：

clear
N=100;
%点随机xdot=rand(N,2);
%点按圆形随机
% r=rand(N,1).^0.3;
% theta=rand(N,1)*2*pi;
% xdot=[r.*cos(theta),r.*sin(theta)];
%点按双行随机
% x=rand(N,1);
% y=[randn(N/2,1)/5+0.5;randn(N/2,1)/5-0.5];
% y(y>1)=1;y(y<-1)=-1;
% y=(y+1)/2.1;
% xdot=[x,y];%点按规则矩形加抖动
% [X1,X2]=meshgrid(0:1/sqrt(N):1-1/sqrt(N));
% xdot=zeros(N,2);
% xdot(:,1)=X1(1:end)'+1/sqrt(N)/2*rand(N,1);
% xdot(:,2)=X2(1:end)'+1/sqrt(N)/2*rand(N,1);%点按随机三角加抖动
% NN=20;
% X1=[];X2=[];
% for j=1:NN
%      if mod(j,2)==0
%          X1=[X1;(0:1/NN/sqrt(3)*2:1-0/NN/sqrt(3)*2)'];
%          X2=[X2;ones(length(0:1/NN/sqrt(3)*2:1-0/NN/sqrt(3)*2),1)*(j-1)/NN];
%      else
%          X1=[X1;(0:1/NN/sqrt(3)*2:1-1/NN/sqrt(3)*2)'+1/NN/sqrt(3)];
%          X2=[X2;ones(length(0:1/NN/sqrt(3)*2:1-1/NN/sqrt(3)*2),1)*(j-1)/NN];
%      end
% end
% N=size(X1,1);
% xdot=[X1+rand(N,1)*1.2/NN/sqrt(3),X2+rand(N,1)*1.2/NN/2];%1Delaulay三角形的构建%整理点，遵循从左到右，从上到下的顺序
xdot=sortrows(xdot,[1 2]);%画出最大包含的三角形
xmin=min(xdot(:,1));xmax=max(xdot(:,1));
ymin=min(xdot(:,2));ymax=max(xdot(:,2));
bigtri=[(xmin+xmax)/2-(xmax-xmin)*1.5,ymin-(xmax-xmin)*0.5;...(xmin+xmax)/2,ymax+(ymax-ymin)+(xmax-xmin)*0.5;...(xmin+xmax)/2+(xmax-xmin)*1.5,ymin-(xmax-xmin)*0.5];xdot=[bigtri;xdot];%点集
edgemat=[1 2 xdot(1,:) xdot(2,:);...2 3 xdot(2,:) xdot(3,:);1 3 xdot(1,:) xdot(3,:)];%边集，每个点包含2个点，4个坐标值
trimat=[1 2 3];%三角集,每个三角包含3个点
temp_trimat=[1 2 3];
for j=4:N+3pointtemp=xdot(j,:);%循环每一个点deltemp=[];%初始化删除temp_trimat的点temp_edgemat=[];%初始化临时边for k=1:size(temp_trimat,1)%循环每一个temp_trimat的三角形panduan=whereispoint(xdot(temp_trimat(k,1),:),...xdot(temp_trimat(k,2),:),xdot(temp_trimat(k,3),:),pointtemp);%判断点在圆内0、圆外1、圆右侧2switch panduancase 0%点在圆内%则该三角形不为Delaunay三角形temp_edge=maketempedge(temp_trimat(k,1),temp_trimat(k,2),temp_trimat(k,3),j,xdot);%把三条边暂时存放于临时边矩阵temp_edgemat=[temp_edgemat;temp_edge];deltemp=[deltemp,k];;case 1%点在圆外，pass;case 2%点在圆右%则该三角形为Delaunay三角形，保存到trianglestrimat=[trimat;temp_trimat(k,:)];%添加到正式三角形中deltemp=[deltemp,k];%并在temp里去除掉%别忘了把正式的边也添加进去edgemat=[edgemat;makeedge(temp_trimat(k,1),temp_trimat(k,2),temp_trimat(k,3),xdot)];%遵循12,13,23的顺序edgemat=unique(edgemat,'stable','rows');end%三角循环结束    end%除去上述步骤中的临时三角形temp_trimat(deltemp,:)=[];temp_trimat(~all(temp_trimat,2),:)=[];%对temp_edgemat去重复temp_edgemat=unique(temp_edgemat,'stable','rows');%将edge buffer中的边与当前的点进行组合成若干三角形并保存至temp triangles中temp_trimat=[temp_trimat;maketemptri(temp_edgemat,xdot,j)];k=k;%点循环结束
end%合并temptri
trimat=[trimat;temp_trimat];
edgemat=[edgemat;temp_edgemat];
%删除大三角形
deltemp=[];
for j=1:size(trimat,1)if ismember(1,trimat(j,:))||ismember(2,trimat(j,:))||ismember(3,trimat(j,:))deltemp=[deltemp,j];end
end
trimat(deltemp,:)=[];
edgemat=[trimat(:,[1,2]);trimat(:,[2,3]);trimat(:,[3,1])];
edgemat=sort(edgemat,2);
edgemat=unique(edgemat,'stable','rows');temp_edgemat=[];
temp_trimat=[];figure(1)
hold on
% plot(xdot(:,1),xdot(:,2),'ko')
for j=1:size(trimat,1)plot([xdot(trimat(j,1),1),xdot(trimat(j,2),1)],[xdot(trimat(j,1),2),xdot(trimat(j,2),2)],'k-')plot([xdot(trimat(j,1),1),xdot(trimat(j,3),1)],[xdot(trimat(j,1),2),xdot(trimat(j,3),2)],'k-')plot([xdot(trimat(j,3),1),xdot(trimat(j,2),1)],[xdot(trimat(j,3),2),xdot(trimat(j,2),2)],'k-')
end
hold off
xlim([0,1]);ylim([0,1]);%凸包监测
%思路是先找出边缘点（三角形只有1个或2个的），顺便整出一个三角形相互关系图，以后用。
%然后顺时针，依次隔一个点连接出一条线段，如果这个和之前的线段相交，则不算；如果不交，则记录出三角形
%更新完了以后，再监测一遍，直到没有新的为止。t_w=0;
while t_w==0[~,border_point,~]=makebordertri(trimat);border_point=[border_point;border_point(1,:)];temp_edgemat=[];temp_trimat=[];for j=1:size(border_point,1)-1tempboderedge=[border_point(j,1),border_point(j+1,2)];tempboderdot=border_point(j,2);%寻找带tempboderdot的所有边tempdotex=edgemat(logical(sum(edgemat==tempboderdot,2)),:);%删除相邻边tempdotex(ismember(tempdotex,[tempboderdot,tempboderedge(1)],'rows'),:)=[];tempdotex(ismember(tempdotex,[tempboderedge(1),tempboderdot],'rows'),:)=[];tempdotex(ismember(tempdotex,[tempboderdot,tempboderedge(2)],'rows'),:)=[];tempdotex(ismember(tempdotex,[tempboderedge(2),tempboderdot],'rows'),:)=[];%检测tempdotex是否为空，如果是证明不用相连t_N=size(tempdotex,1);t_t=0;if t_N>0%依次检测是否相交，只要有一个相交就不算；如果都不想交，则相连for k=1:t_Nif tempdotex(k,1)==tempboderdott_xdotno4=tempdotex(k,2);elset_xdotno4=tempdotex(k,1);endtt_xdotno4=xdot(t_xdotno4,:)-xdot(tempboderdot,:);xdotno4=xdot(tempboderdot,:)+tt_xdotno4/sqrt(sum(tt_xdotno4.^2))*(sqrt((xmax-xmin)^2+(ymax-ymin)^2));panduan=crossornot(xdot(tempboderedge(1),:),xdot(tempboderedge(2),:),xdot(tempboderdot,:),xdotno4);if panduan==1t_t=t_t+1;breakendend%t_t大于0说明有相交的线,略过if t_t==0temp_edgemat=[temp_edgemat;tempboderedge];temp_trimat=[temp_trimat;[tempboderedge,tempboderdot]];breakendendendtrimat=[trimat;temp_trimat];edgemat=[edgemat;temp_edgemat];%删除重复的三角形trimat=sort(trimat,2);trimat=unique(trimat,'stable','rows');if j==size(border_point,1)-1t_w=1;end
endfigure(2)
hold on
% plot(xdot(:,1),xdot(:,2),'ko')
for j=1:size(trimat,1)plot([xdot(trimat(j,1),1),xdot(trimat(j,2),1)],[xdot(trimat(j,1),2),xdot(trimat(j,2),2)],'k-')plot([xdot(trimat(j,1),1),xdot(trimat(j,3),1)],[xdot(trimat(j,1),2),xdot(trimat(j,3),2)],'k-')plot([xdot(trimat(j,3),1),xdot(trimat(j,2),1)],[xdot(trimat(j,3),2),xdot(trimat(j,2),2)],'k-')
end
hold off
xlim([0,1]);ylim([0,1]);%2泰森多边形的建立步骤
%求每个三角形的外接圆圆心trimatcenter=zeros(size(trimat,1),2);
for j=1:size(trimat,1)[a,b,~]=maketricenter(xdot(trimat(j,1),:),xdot(trimat(j,2),:),xdot(trimat(j,3),:));trimatcenter(j,:)=[a,b];
end%求三角形的相邻三角形个数
[border_trimat,border_point,trimat_con]=makebordertri(trimat);
Thi_edge1=[];
for j=1:size(trimat,1)tempedge=[];%第一个相邻三角形if trimat_con(j,1)~=0tempedge=[tempedge;[j,trimat_con(j,1)]];end%第二个相邻三角形if trimat_con(j,2)~=0tempedge=[tempedge;[j,trimat_con(j,2)]];end%第三个相邻三角形if trimat_con(j,3)~=0tempedge=[tempedge;[j,trimat_con(j,3)]];endThi_edge1=[Thi_edge1;tempedge];
end%绘制非边缘泰勒多边形
figure(3)
Thi_edge1=unique(Thi_edge1,'stable','rows');
xlim([0,1]);ylim([0,1]);
hold on
for j=1:size(Thi_edge1,1)plot(trimatcenter([Thi_edge1(j,1),Thi_edge1(j,2)],1),trimatcenter([Thi_edge1(j,1),Thi_edge1(j,2)],2),'color',[0,0.4,0])
end%绘制边缘泰勒多边形
%先逐个边试探，如果中心点在三角内，则做中心-边缘延长线
%如果中心点在三角外，如果在屏幕外，忽略，如果在屏幕内，做边缘-中心延长线for j=1:size(border_point,1)%先找到边对应的三角temp_trimat=border_trimat(sum(border_trimat==border_point(j,1),2)+sum(border_trimat==border_point(j,2),2)==2,:);%判断中心点是否在三角形内[t_x1,t_y1,~]=maketricenter(xdot(temp_trimat(1),:),xdot(temp_trimat(2),:),xdot(temp_trimat(3),:));%求中心panduan=pointintriangle(xdot(temp_trimat(1),:),xdot(temp_trimat(2),:),xdot(temp_trimat(3),:),[t_x1,t_y1]);%求边的中点t_x2=(xdot(border_point(j,1),1)+xdot(border_point(j,2),1))/2;t_y2=(xdot(border_point(j,1),2)+xdot(border_point(j,2),2))/2;if panduan==1%做中心-边缘的延长线%这里用到了边缘在01这个条件t_xy3=[t_x1,t_y1]+[t_x2-t_x1,t_y2-t_y1]*sqrt(2)/sqrt((t_x2-t_x1)^2+(t_y2-t_y1)^2);plot([t_x1,t_xy3(1)],[t_y1,t_xy3(2)],'color',[0,0.4,0])elseif ~(t_x1<0||t_x1>1||t_y1<0||t_y1>1)%判断点是否在边与边框的三角内，如果在，做中心的延长线%如果不在，做中心-边缘的延长线%或者改成判断点是否在多边形内panduan2=pointinmutiangle(xdot,[border_point(1,1);border_point(:,2)],[t_x1,t_y1]);if panduan2==1t_xy3=[t_x1,t_y1]+[t_x2-t_x1,t_y2-t_y1]*sqrt(2)/sqrt((t_x2-t_x1)^2+(t_y2-t_y1)^2);plot([t_x1,t_xy3(1)],[t_y1,t_xy3(2)],'color',[0,0.4,0])elset_xy3=[t_x1,t_y1]+[t_x1-t_x2,t_y1-t_y2]*1/sqrt((t_x2-t_x1)^2+(t_y2-t_y1)^2);plot([t_x1,t_xy3(1)],[t_y1,t_xy3(2)],'color',[0,0.4,0])endend
endscatter(xdot(:,1),xdot(:,2),5,[0,0.4,0],'filled')
hold off%判断点在三角形外接圆的哪个部分
function panduan=whereispoint(xy1,xy2,xy3,xy0)
%判断点在三角形外接圆的哪个部分
[a,b,r2]=maketricenter(xy1,xy2,xy3);
x0=xy0(1);y0=xy0(2);
if a+sqrt(r2)<x0%x0在圆的右侧panduan=2;
elseif (x0-a)^2+(y0-b)^2<r2%x0在圆内panduan=0;
else%在圆外panduan=1;
end
end%做出三角形三点与内部1点之间的线段
function temp_edge=maketempedge(dot1,dot2,dot3,dot0,xdot)
%做出连接点与三角形之间的线
%每行包含2个点，4个坐标值，共3行
%xy1和xy0组成线段
temp_edge=zeros(3,6);
if xdot(dot1,1)<xdot(dot0,1)temp_edge(1,:)=[dot1,dot0,xdot(dot1,:),xdot(dot0,:)];
elseif xdot(dot1,1)==xdot(dot0,1)if xdot(dot1,2)<xdot(dot0,2)temp_edge(1,:)=[dot1,dot0,xdot(dot1,:),xdot(dot0,:)];elsetemp_edge(1,:)=[dot0,dot1,xdot(dot0,:),xdot(dot1,:)];end
elsetemp_edge(1,:)=[dot0,dot1,xdot(dot0,:),xdot(dot1,:)];
end
%xy2和xy0组成线段
if xdot(dot2,1)<xdot(dot0,1)temp_edge(2,:)=[dot2,dot0,xdot(dot2,:),xdot(dot0,:)];
elseif xdot(dot2,1)==xdot(dot0,1)if xdot(dot2,2)<xdot(dot0,2)temp_edge(2,:)=[dot2,dot0,xdot(dot2,:),xdot(dot0,:)];elsetemp_edge(2,:)=[dot0,dot2,xdot(dot0,:),xdot(dot2,:)];end
elsetemp_edge(2,:)=[dot0,dot2,xdot(dot0,:),xdot(dot2,:)];
end
%xy3和xy0组成线段
if xdot(dot3,1)<xdot(dot0,1)temp_edge(3,:)=[dot3,dot0,xdot(dot3,:),xdot(dot0,:)];
elseif xdot(dot3,1)==xdot(dot0,1)if xdot(dot3,2)<xdot(dot0,2)temp_edge(3,:)=[dot3,dot0,xdot(dot3,:),xdot(dot0,:)];elsetemp_edge(3,:)=[dot0,dot3,xdot(dot0,:),xdot(dot3,:)];end
elsetemp_edge(3,:)=[dot0,dot3,xdot(dot0,:),xdot(dot3,:)];
endend%做出一些列固定点发散的线段外点组成的三角形
function temp_trimat=maketemptri(temp_edgemat,xdot,dot0)
%将edge buffer中的边与当前的点进行组合成若干三角形
%temp_edgemat是新边，x是中心点
%思路是计算各个边对应角度，然后排序相连A=temp_edgemat(:,1:2);
pointline=A(A~=dot0);
N=length(pointline);
pointaxe=xdot(pointline,:);
img_pointaxe=pointaxe(:,1)+1i*pointaxe(:,2);
d_img_pointaxe=img_pointaxe-xdot(dot0,1)-1i*xdot(dot0,2);
angle_d_img_pointaxe=angle(d_img_pointaxe);
[~,index]=sort(angle_d_img_pointaxe);
index=[index;index(1)];%排序，然后依次串起来
temp_trimat=zeros(N,3);
for j=1:Ntemp_trimat(j,:)=[pointline(index(j)),pointline(index(j+1)),dot0];
endend%将三个点构成3条边
function edgemat=makeedge(dot1,dot2,dot3,xdot)
%将dot1 2 3这三个点构成三条边
%每行包含2个点，4个坐标值，共3行
edgemat=zeros(3,6);
%点12
if xdot(dot1,1)<xdot(dot2,1)edgemat(1,:)=[dot1,dot2,xdot(dot1,:),xdot(dot2,:)];
elseif xdot(dot1,1)==xdot(dot2,1)if xdot(dot1,2)<xdot(dot2,2)edgemat(1,:)=[dot1,dot2,xdot(dot1,:),xdot(dot2,:)];elseedgemat(1,:)=[dot2,dot1,xdot(dot2,:),xdot(dot1,:)];end
elseedgemat(1,:)=[dot2,dot1,xdot(dot2,:),xdot(dot1,:)];
end
%点13
if xdot(dot1,1)<xdot(dot3,1)edgemat(2,:)=[dot1,dot3,xdot(dot1,:),xdot(dot3,:)];
elseif xdot(dot1,1)==xdot(dot3,1)if xdot(dot1,2)<xdot(dot3,2)edgemat(2,:)=[dot1,dot3,xdot(dot1,:),xdot(dot3,:)];elseedgemat(2,:)=[dot3,dot1,xdot(dot3,:),xdot(dot1,:)];end
elseedgemat(2,:)=[dot3,dot1,xdot(dot3,:),xdot(dot1,:)];
end
%点23
if xdot(dot3,1)<xdot(dot2,1)edgemat(3,:)=[dot3,dot2,xdot(dot3,:),xdot(dot2,:)];
elseif xdot(dot3,1)==xdot(dot2,1)if xdot(dot3,2)<xdot(dot2,2)edgemat(3,:)=[dot3,dot2,xdot(dot3,:),xdot(dot2,:)];elseedgemat(3,:)=[dot2,dot3,xdot(dot2,:),xdot(dot3,:)];end
elseedgemat(3,:)=[dot2,dot3,xdot(dot2,:),xdot(dot3,:)];
end
% edgemat
end%求三角形外接圆圆心
function [a,b,r2]=maketricenter(xy1,xy2,xy3)
x1=xy1(1);y1=xy1(2);
x2=xy2(1);y2=xy2(2);
x3=xy3(1);y3=xy3(2);
a=((y2-y1)*(y3*y3-y1*y1+x3*x3-x1*x1)-(y3-y1)*(y2*y2-y1*y1+x2*x2-x1*x1))/(2.0*((x3-x1)*(y2-y1)-(x2-x1)*(y3-y1)));
b=((x2-x1)*(x3*x3-x1*x1+y3*y3-y1*y1)-(x3-x1)*(x2*x2-x1*x1+y2*y2-y1*y1))/(2.0*((y3-y1)*(x2-x1)-(y2-y1)*(x3-x1)));
r2=(x1-a)*(x1-a)+(y1-b)*(y1-b);
end%求边缘三角形
function [border_trimat,border_point,trimat_con]=makebordertri(trimat)
N=size(trimat,1);
border_trimat=[];
border_point=[];
trimat_con=zeros(N,3);
for j=1:N%tempborder_trimat=zeros(3,3);temptri=trimat(j,:);%计算temptri中12点边对应的三角形有哪些edgetrimat=find(sum(trimat==temptri(1),2)+sum(trimat==temptri(2),2)==2);edgetrimat(edgetrimat==j)=[];if size(edgetrimat,2)==0%这个边没有三角形相连，是个临边。border_point=[border_point;[temptri(1),temptri(2)]];elseif size(edgetrimat,2)==1%这个边没有三角形相连，是个临边。%tempborder_trimat(1,:)=trimat(edgetrimat,:);%记录三角形三点坐标trimat_con(j,1)=edgetrimat;%trimat_con记录上相邻三角形end%计算temptri中23点边对应的三角形有哪些edgetrimat=find(sum(trimat==temptri(2),2)+sum(trimat==temptri(3),2)==2);edgetrimat(edgetrimat==j)=[];if size(edgetrimat,2)==0border_point=[border_point;[temptri(2),temptri(3)]];elseif size(edgetrimat,2)==1%tempborder_trimat(2,:)=trimat(edgetrimat,:);trimat_con(j,2)=edgetrimat;end%计算temptri中31点边对应的三角形有哪些edgetrimat=find(sum(trimat==temptri(3),2)+sum(trimat==temptri(1),2)==2);edgetrimat(edgetrimat==j)=[];if size(edgetrimat,2)==0border_point=[border_point;[temptri(3),temptri(1)]];elseif size(edgetrimat,2)==1%tempborder_trimat(3,:)=trimat(edgetrimat,:);trimat_con(j,3)=edgetrimat;end%tempborder_trimat(all(tempborder_trimat==0, 2),:)=[];%删除0行if ~all(trimat_con(j,:))%如果边缘三角少于3个,就添加border_trimat=[border_trimat;temptri];endend%把边首尾排序一遍,输出border_point
for j=1:size(border_point,1)-1border_pointtemp=find(sum(border_point==border_point(j,2),2)==1);border_pointtemp(border_pointtemp==j)=[];border_point([j+1,border_pointtemp],:)=border_point([border_pointtemp,j+1],:);if border_point(j,2)==border_point(j+1,2)border_point(j+1,[1,2])=border_point(j+1,[2,1]);end
endend%判断两个线段是否相交
function panduan=crossornot(l1xy1,l1xy2,l2xy1,l2xy2)
l1x1=l1xy1(1);l1y1=l1xy1(2);
l1x2=l1xy2(1);l1y2=l1xy2(2);
l2x1=l2xy1(1);l2y1=l2xy1(2);
l2x2=l2xy2(1);l2y2=l2xy2(2);
%先快速判断
if    (max(l2x1,l2x2)<min(l1x1,l1x2))||(max(l2y1,l2y2)<min(l1y1,l1y2))||...(max(l1x1,l1x2)<min(l2x1,l2x2))||(max(l1y1,l1y2)<min(l2y1,l2y2))%如果判断为真，则一定不会相交panduan=0;
else%如果判断为假，进一步差积判断if ((((l1x1-l2x1)*(l2y2-l2y1)-(l1y1-l2y1)*(l2x2-l2x1))*...((l1x2-l2x1)*(l2y2-l2y1)-(l1y2-l2y1)*(l2x2-l2x1))) > 0 ||...(((l2x1-l1x1)*(l1y2-l1y1)-(l2y1-l1y1)*(l1x2-l1x1))*...((l2x2-l1x1)*(l1y2-l1y1)-(l2y2-l1y1)*(l1x2-l1x1))) > 0)%如果判断为真，则不会相交panduan=0;elsepanduan=1;end
end
end%两个向量做差积
function t=crossdot(xy1,xy2)
x1=xy1(1);y1=xy1(2);
x2=xy2(1);y2=xy2(2);
t=x1*y2-y1*x2;
end%点是否在三角形内
function panduan=pointintriangle(xy1,xy2,xy3,xy0)
x1=xy1(1);y1=xy1(2);
x2=xy2(1);y2=xy2(2);
x3=xy3(1);y3=xy3(2);
x0=xy0(1);y0=xy0(2);
PA=[x1-x0,y1-y0];PB=[x2-x0,y2-y0];PC=[x3-x0,y3-y0];
%利用差积同正或同负号来判断是否在三角内
t1=crossdot(PA,PB);
t2=crossdot(PB,PC);
t3=crossdot(PC,PA);
if abs(sign(t1)+sign(t2)+sign(t3))==3panduan=1;
elsepanduan=0;
endend%点是否在多边形内
function panduan=pointinmutiangle(xdot,d_no,xy0)
%d_no符合12341的格式，收尾相连
Ndot=xdot(d_no,:);
PN=[Ndot(:,1)-xy0(1),Ndot(:,2)-xy0(2)];
tn=zeros(length(d_no)-1,1);
for j=1:length(d_no)-1tn(j)=crossdot(PN(j,:),PN(j+1,:));
end
%利用差积同正或同负号来判断是否在三角内if abs(sum(sign(tn)))==length(d_no)-1panduan=1;
elsepanduan=0;
endend

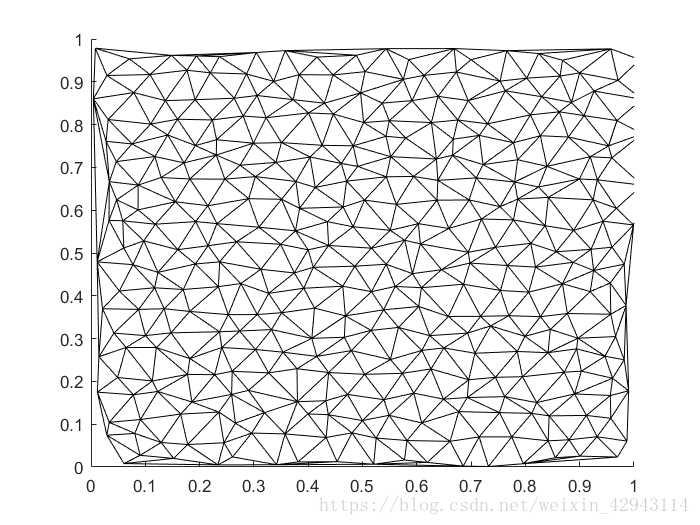
最终得到的图形如下：

Delaunay三角网格

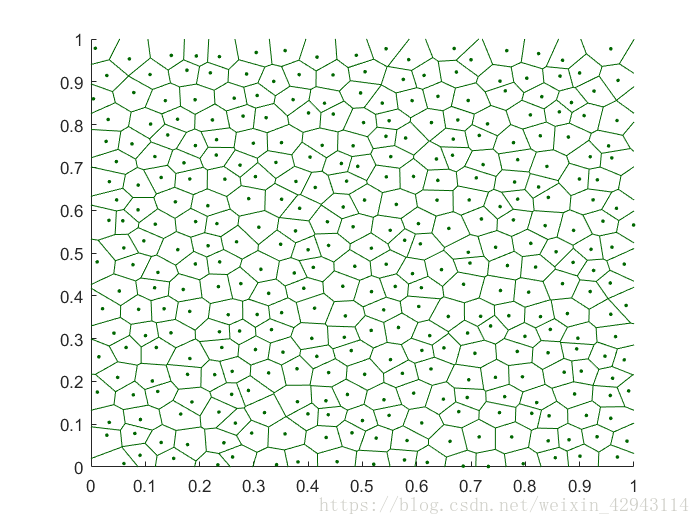
Voronoi图