您现在的位置是:主页 > news > 苏州建设局网站/seo排名工具哪个好
苏州建设局网站/seo排名工具哪个好
![]() admin2025/5/5 6:11:15【news】
admin2025/5/5 6:11:15【news】
简介苏州建设局网站,seo排名工具哪个好,公司网站首页怎么制作,国内做网站群平台的公司点击上方蓝色字体“高中数学王晖”关注王晖老师,免费获取各种知识干货和学习经验~~~您的点赞转发是对老师的最大鼓舞~~~距高考还有35天函数的极值我这样理解极值相关概念:➤极值点不是一个点,而是点的横坐标(类似零点概念);➤函数…
点击上方蓝色字体“高中数学王晖”关注王晖老师,免费获取各种知识干货和学习经验~~~您的点赞转发是对老师的最大鼓舞~~~
距高考还有35天
函数的极值

我这样理解极值相关概念:
➤极值点不是一个点,而是点的横坐标(类似零点概念);➤函数的极值点可能不唯一,有时会有多个;➤定义域端点一定不是极值点,端点的函数值一定不是极值;➤极值是函数局部性质,是在定义域某一局部范围内的最大值或最小值;➤函数的最大值为MAX{极值、边界函数值}最小值为MIN{极值、边界函数值};➤极值点原本与导数无关;1

1
认识两个假命题
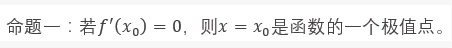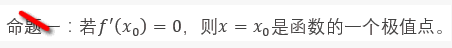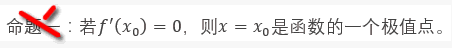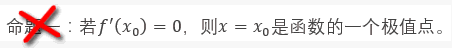

函数在极值点处一定取图像局部的最高点或最低点。而导数为0,则只能说明函数在该点处的切线是水平的,并不能代表这个点就一定最高或最低。

典例讲解



 函数在极值点处一定是图像局部的最高点或最低点。但并不能说明函数在该点处导数就一定存在取,只有导数存在时,极值点处的导数值才等于0。
函数在极值点处一定是图像局部的最高点或最低点。但并不能说明函数在该点处导数就一定存在取,只有导数存在时,极值点处的导数值才等于0。
“圆点可导,尖点不可导”,是指曲线只有在圆点处才会存在切线,而尖点处是不存在切线的。

那么,从这两个假命题我们就不难看出,函数“在某点处的导数值为0”,应该是“该点为极值点”的既不充分也不必要条件。
当然,对于可导函数来说,函数“在某点处的导数值为0”,应该是“该点为极值点”的必要不充分条件。

2
极值与最值的关系
 其实,极值与最值的关系是很好理解的,极值是函数局部范围的最大或最小值。而最值,是函数在整个定义域内的最大或最小值。极值一定在定义域内部产生,而最值,有可能是函数在定义域端点处的函数值。因此,求函数的最值,只需求出函数的全体极值以及端点函数值,再进行比较,最大的为函数最大值,最小的,为函数最小值。
其实,极值与最值的关系是很好理解的,极值是函数局部范围的最大或最小值。而最值,是函数在整个定义域内的最大或最小值。极值一定在定义域内部产生,而最值,有可能是函数在定义域端点处的函数值。因此,求函数的最值,只需求出函数的全体极值以及端点函数值,再进行比较,最大的为函数最大值,最小的,为函数最小值。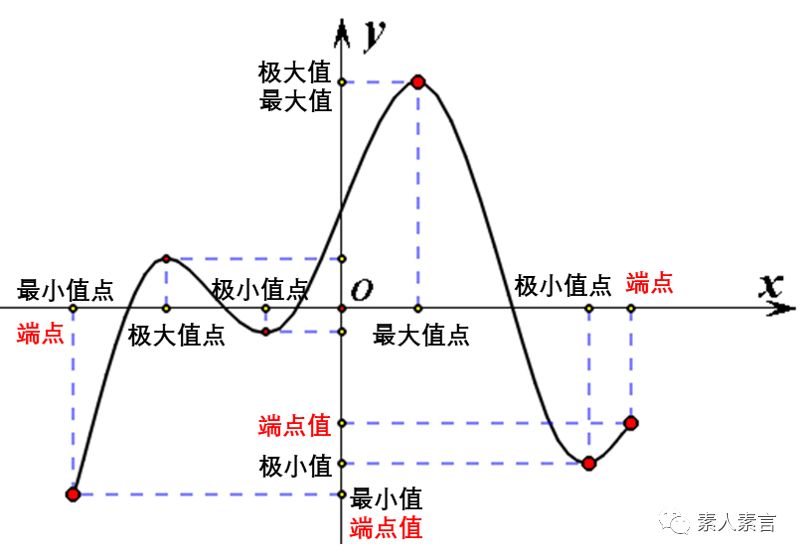 图解极值与最值
图解极值与最值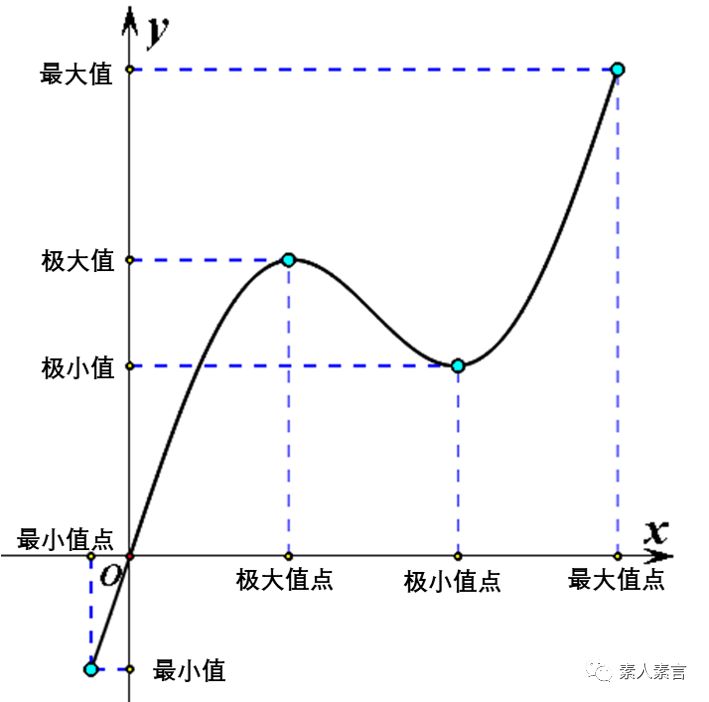

3
从极值到“拉格朗日乘数法”
 如果从函数的角度来说,我们一般把含一个自变量的函数称为一元函数,也就是我们现在所常见的函数了;如果一个函数含有两个自变量,我们称之为二元函数,可以以此类推。一元函数的图像是曲线,二元函数的图像在三维空间里应该就是曲面了。一元函数的极值点是函数图像的拐弯点,也就是增减区间的分界点,那二元函数呢?曲面的“拐弯”点依然叫做极值点。如下图:
如果从函数的角度来说,我们一般把含一个自变量的函数称为一元函数,也就是我们现在所常见的函数了;如果一个函数含有两个自变量,我们称之为二元函数,可以以此类推。一元函数的图像是曲线,二元函数的图像在三维空间里应该就是曲面了。一元函数的极值点是函数图像的拐弯点,也就是增减区间的分界点,那二元函数呢?曲面的“拐弯”点依然叫做极值点。如下图: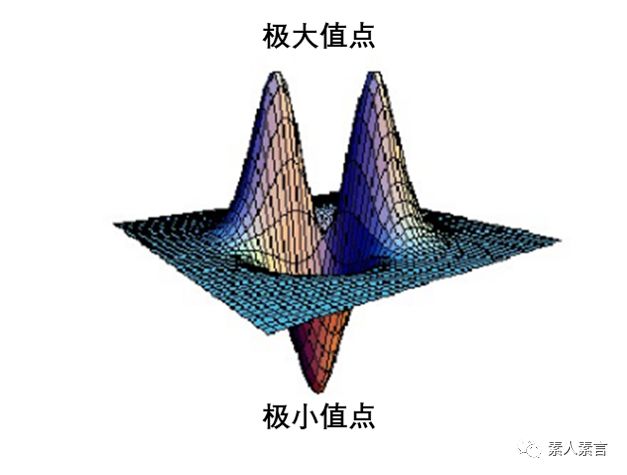 二元函数极值点
二元函数极值点 当然和一元函数一样也并不是所有的二元函数都有极值点的
当然和一元函数一样也并不是所有的二元函数都有极值点的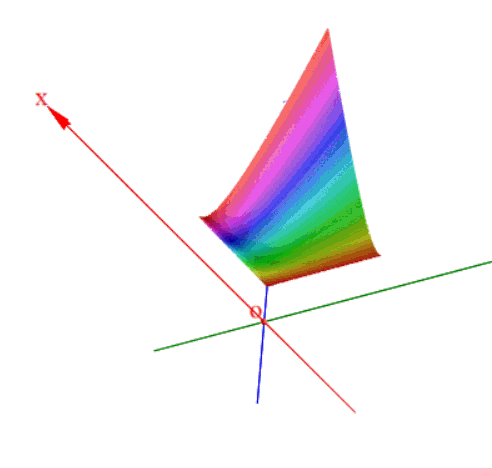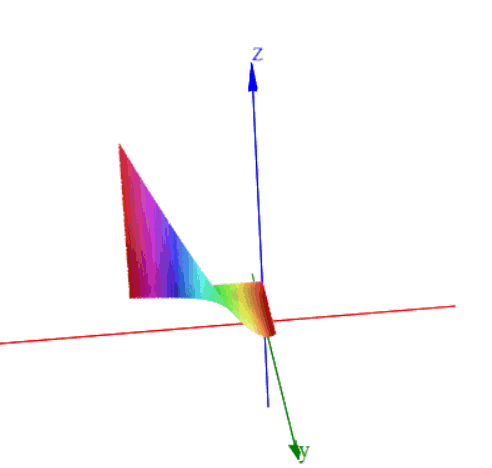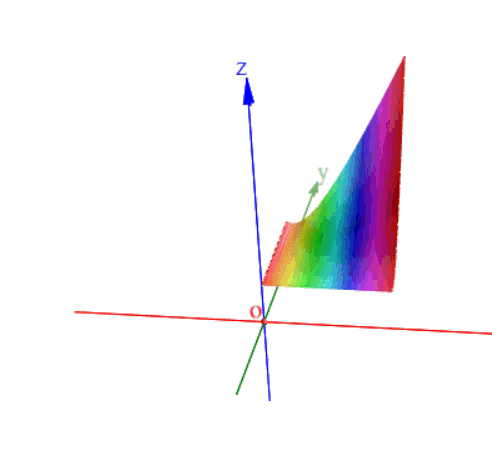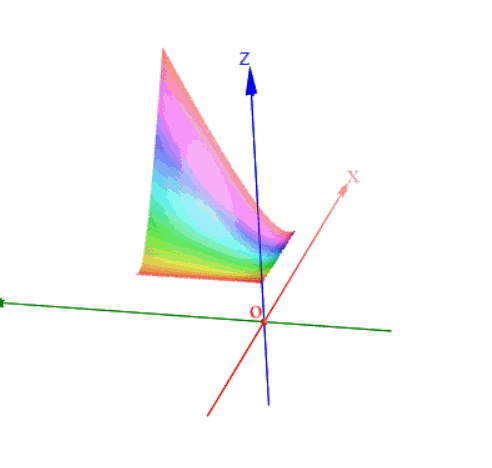
 在我们考试时,是不是经常会遇见让人头疼的二元代数式的最值问题呢?其实,我们如果从二元函数极值的角度去进行思考,就很方便了。我们就直接看例子。不过在例题之前,还是要先了解一个概念——偏导数。在数学中,一个多变量函数的偏导数,就是它关于其中一个变量的导数而保持其他变量恒定。
在我们考试时,是不是经常会遇见让人头疼的二元代数式的最值问题呢?其实,我们如果从二元函数极值的角度去进行思考,就很方便了。我们就直接看例子。不过在例题之前,还是要先了解一个概念——偏导数。在数学中,一个多变量函数的偏导数,就是它关于其中一个变量的导数而保持其他变量恒定。
dvdf
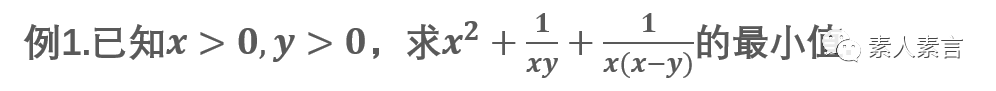



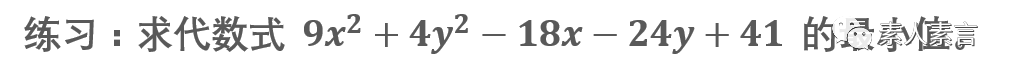
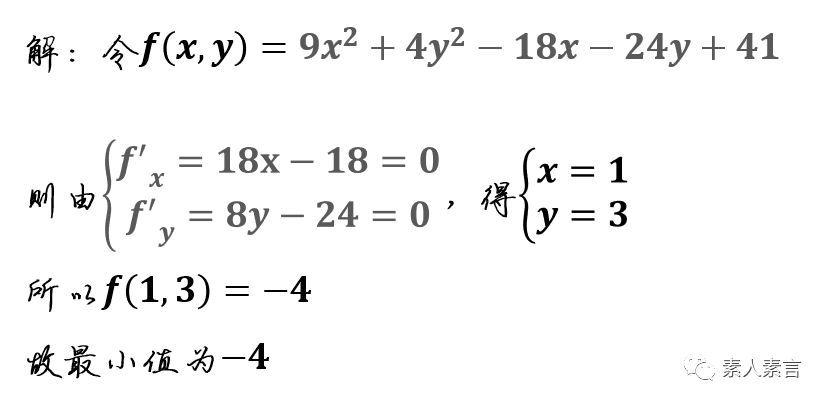
 特别说明:和一元函数极值点与该点处导数为0之间的关系相类似,两者并不等价,但在高中阶段,一般情况下计算出的结果即为最值。
特别说明:和一元函数极值点与该点处导数为0之间的关系相类似,两者并不等价,但在高中阶段,一般情况下计算出的结果即为最值。
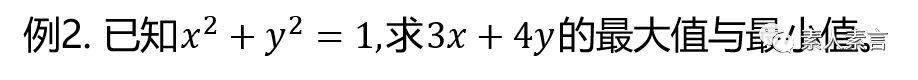



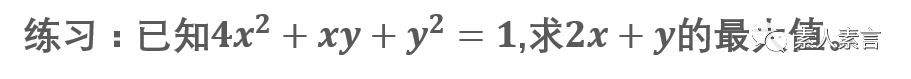


往期优质数学干货链接:
【风雨同舟】平面向量等和线------这些巧妙的运用你都知道吗???
【焕然一新】立体几何“翻折问题”的解题策略------如何在“变”与“不变”中找到平衡点!!!
【安心定志】双重变量的最值问题------“主元法”是一种不错的选择!!!
【础润而雨】大师用实例告诉你何为“对偶式”------它真是好用、易学又简便!!!
【山清水秀】一个小小的三角形居然隐藏了这么多的秘密------这些都是必须掌握的!!!









